Digital Information - Lesson 5: Overflow and Rounding

Overview

Students extend their understanding of the binary number system by exploring errors that result from overflow and rounding. They make a "flippy do pro" to practice binary-to-decimal number conversions which include fractional place values.

Goals

Students will be able to:

• Describe how to include fractions in the binary number system.
• Understand that overflow and roundoff errors result from real-world limitations in representing place value.

Purpose

This lesson introduces students to the practical aspects of using a binary system to represent numbers in a computing device. Students discover the limitations of creating numbers that are "too big" or "too small" to count. They learn that, while a number system is infinite, the physical representation of numbers requires place values -- which are finite, and limit the ability to represent numbers.When using this binary representation of numbers, certain values (1, 2, 4, 8, 16, etc.) are seen repeatedly. When written in binary, these values are 1, 10, 100, 1000, 10000, and so on, and so are the incremental place values in this binary number system.

Resources

Supplemental Code.org material

• Flippy Do Pro worksheet in print
• Flippy Do Pro worksheet in braille, Duxbury file
• Flippy Do Pro worksheet in braille, .brf

Getting Started (5 minutes)

Discuss: Imagine you work at a local store. In the register all you have are nine $10 bills, nine $1 bills, and nine dimes.

• What's the largest amount of change that you can give someone?
• What's the least?
• What would you do if someone needed 7 cents in change?

Discussion Goal: Today we're going to explore what happens when you don't have the right "places" to store information. This can happen when you try to store very large numbers, very small ones, and everything in-between! The goal of the prompt is to understand the very real problem of making sure that enough place values are available to represent numbers.

• The largest amount of change you can give someone is $99.90.
• The least change you can give is $0.10.
• You can't give someone $0.07. You also can't give someone $1.25 in change (because you have no nickels!)

At both extremes of the number range, large and small -- and in between numbers -- you are unable to build some numbers because you don't have the place values to do so.

Activity (35 mins)

Place students in groups of two. Groups will need one computer per group.

Prompt: Suppose we have a car odometer. The number in the odometer keeps going up as we drive. What about when the odometer reaches the max value? What happens if we keep driving?

Flippy Do Pro

• Now that you have started thinking about place value and overflow, we are going to work on a different problem. What happens when there aren't enough place values to represent a number? You will explore this with a new version of the Flippy Do, the Flippy Do Pro!

Provide each group with a copy of the Flippy Do Pro Template and scissors.

Do This: Cut and fold your Flippy Do Pro following the guidance on the slide. Fill out all the numbers if they are not already done.

Remarks

• The Flippy Do Pro is similar to the one you made before. But this time, the Flippy Do Pro is already filled with binary place values assigned in a different way -- they include fractions.
• When using the Flippy Do Pro, the numbers on the left-hand side of the line are whole numbers and those on the right-hand side of the line are fractional numbers.

Teaching Tip

• The Flippy Do Pro is still using 8 bits to represent a number. But this time, the place value of each bit has been assigned in a different way than in the previous Flippy Do. The bits have been "shifted" to the right two times. The value 1 (2^0) is no longer the smallest place value. The value of a bit just to the right of 1 (2^0) is 0.5, which is 2^-1. The value to the right again is 0.25 which is 2^-2.
• Students may struggle with negative exponents. What's more important than emphasizing the math is emphasizing the pattern of place values in the Flippy Do Pro. As you move left, the place value doubles. As you move right, the place value halves.
• Help students see that using the Flippy Do Pro is similar to using the Flippy Do. To form a value, flip the flaps up or down at the bottom of the device to create a sequence of zeros and ones. Note that the range of place values is limited by the largest bit value, 2^5 which is 32, and the smallest bit value, 2^-2 which is 0.25. As with the Flippy Do, adding together all the values for each place value containing a "1" produces the total value represented on the Flippy Do Pro.

Flippy Do Pro Challenges

Challenge #1 - Smallest Number: Produce the smallest binary number possible with the Flippy Do Pro.

• The smallest binary number students produce is 000000.01 and this number has a decimal value of 0.25.

Challenge #2 - Next Value: Increase the number made in Challenge #1 to the next possible value.

• The binary number students produce is 000000.10 and this number has a decimal value of 0.50.

Challenge #3 - Got Quarters? Make the values 0.25, 0.50, and 0.75 one after another.

• The binary numbers students produce are 000000.01, 000000.10, 000000.11. Note the pattern of changing a place value from 1 to 0 and then "carrying" the one.

Challenge #4 - Can't Make Change: Make all the fractional possible in binary using the Flippy Do Pro.

• There are no new values besides those made in Challenge #3 because there are no place values for representing other fractions.
• Note, if students need a concrete example for Challenge #4, have them try to make 39 cents in binary. It can't be done with the values they have available in the Flippy Do Pro.

Challenge #5 - Largest Number: What is the largest number (in decimal) you can make with the Flippy Do Pro?

• With all of the bits flipped to 1, the largest number you can make is 63.75. Note that this is smaller than the largest you can make with a traditional Flippy Do, which is 255. This is because we have shifted two bits to represent smaller numbers (0.5 & 0.25).

Challenge #6 - How Much Pie: Challenge 6 contains a number of pie charts. Each chart has a single colored slice, representing a piece of pie. Students use a Flippy Do Pro to determine how much pie is left at the end of dessert. With each slide, allow time for students to decide how to represent the amount of pie left as a binary number, then convert that to decimal and write it down in the journal. In this challenge it is expected that students will estimate and do some rounding when determining how much pie is left.

Do This: For each pie chart, students should:

1. Estimate how big the colored slice is.
2. Use your Flippy Do Pro to represent how big the slice is. You may need to round up or down.
3. Convert your binary number to a decimal number.
4. Write down the number in your journal.

Pie #1: Pumpkin

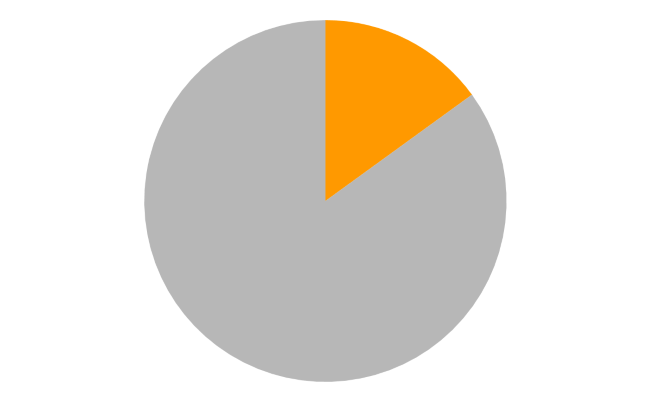
Pie #2: Cherry

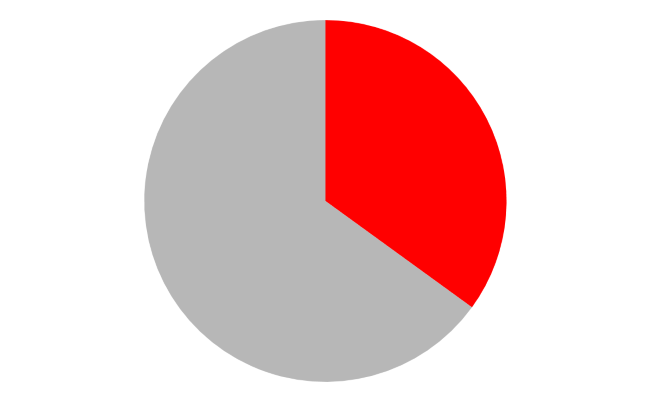
Pie #3: Lemon

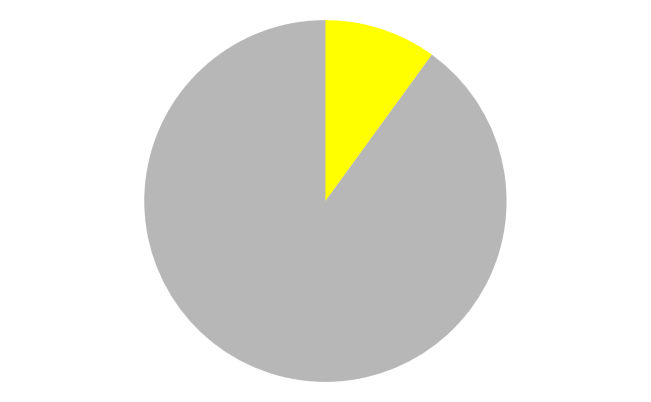
Pie #4: Chocolate

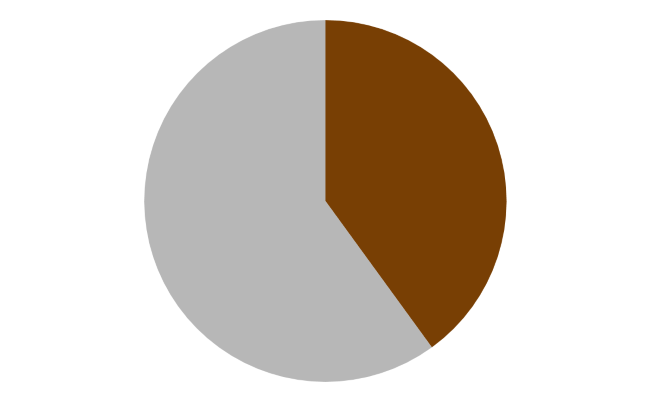
Do This: Add all the decimal numbers together. Compare with a partner and discuss.

Final Task

• In our final challenge, your answer may be different than your classmates. It comes down to how you rounded - did you decide to round up or round down with the various amounts of pie. If we did not have to round, the answer would be exactly one pie left over. You may have come to the same conclusion by rounding - or not!

Prompt: Why is it a problem for a computer if your answers are different than others?

Discussion Goal: Computers rely on precision. Think of a calculator. We depend on 1+1 always equaling 2. Rounding is necessary because of the limits of bits, but can lead to errors.

Wrap up (5 Minutes)

Review the information on the first wrapup slide showing how binary can be used to precisely represent some fractional values from the decimal number system. Students do not need to understand how to convert fractional amounts from decimal to binary.

Remarks

• The most important takeaway from this lesson is to understand that bits can represent a limited amount of information.

Discuss

• What does an odometer show us about representing large numbers?
• What does the Flippy Do Pro show about representing very small numbers?
• If we had a big enough odometer or Flippy Do Pro, could we represent every possible number?

Discussion Goal

As students have seen, you can make "any number" in your head, but the tool you use to represent a number has limitations. It has a fixed number of place values it can show. An odometer keeps running after you move beyond its upper limit, but the largest place values cannot be displayed due to overflow error.

In the Flippy Do Pro, you assigned some of the bits to fractions, but you saw that you still couldn't represent certain "small" numbers -- you could only show a number that was "close to" your target number. This is roundoff error, an error that occurs when bit arrangements can't represent numbers as intended.

Ultimately, regardless of the size of our odometer or Flippy Do Pro, and how many bits we add to them, there's going to be numbers that are too large, too small, or "in-between" the values we want to represent.

Journal

Students add to their journals the definitions for: Overflow Error and Round-off Error.

• Overflow Error: Error from attempting to represent a number that is too large.
• Round-off Error: Error from attempting to represent a number that is too precise. The value is rounded.

Assessment: Check for Understanding

For Students

Open a word doc or google doc and copy/paste the 3 following question.

Question 1

Modern car odometers record up to a million miles driven. What happens to the odometer reading when a car drives beyond its maximum reading?

Question 2

When using bits to represent fractions of a number, can you create all possible fractions? Why or why not?

Standards Alignment

• CSTA K-12 Computer Science Standards (2017): DA - Data & Analysis: 3A-DA-09 - Translate between different bit representations of real-world phenomena, such as characters, numbers, and images.
• CSP2021: DAT-1.B.1, DAT-1.B.2, DAT-1.B.3

Next Tutorial

In the next tutorial, we will discuss CSP Internet Lesson 6 (Optional), which describes how work Tortoise vs. the Hare in Quorum..