Algorithms - Lesson 2: Algorithm Efficiency
Overview
In this lesson students follow a demonstration of Linear Search before writing their own search algorithms. Following this, students are introduced to Binary Search after which they compare graphs of the search algorithms to determine which is most efficient.
Goals
Students will be able to:
- Use Linear Search to determine if a number is in a list
- Use Binary Search to determine if a number is in a list
- Compare the efficiency of Linear Search and Binary Search
Purpose
In the previous lesson students learned that there are many different ways to write an algorithm to solve a problem. However, not all solutions are good options, and some algorithms require many fewer steps to run than others. This lesson focuses on comparing Linear Search to Binary Search. The the length of the list being searched, the more efficient Binary Search is compared to Linear Search. That said, Binary Search has a constraint: the list must first be sorted. This lesson more broadly introduces students to thinking about the efficiency of an algorithm, an idea that will be explored more in future lessons.
Getting Started (5 minutes)
Prompt: Have you ever lost a pencil in a backpack? What are the steps you take to find the pencil?
Discuss: Have students think about their answers on their own, then share with a partner, and then finally discuss responses with the entire room.
Discussion Goal
Use this discussion to highlight the following points
- Students may have as systematic approach (search through every pocket in order) or a random approach.
- Some students may have a system where they place their books and materials in their backpack to be retrieved in the order of their class schedule. If they look in their bag at a certain spot and don't see the pencil, they have a pretty good idea where to search next.
- There are no right answers here - the idea is to start thinking about the efficiency of different search methods.
Remarks
- There are many different ways to achieve the same goal for this problem: finding your pencil. Today we are going to explore different search methods that computers use.
Activity (30 minutes)
Distribute: Students should have their journals. They will also need somewhere to record numbers, such as on sticky notes.
Open a Project: Have students open the Lesson2_TicketGenerator project in the Unit 6 folder of the CSP-Widgets repository. Students will use this to randomly generate ticket numbers for today's activity.
Do This: Call for three volunteers. These students use the Ticket Generator program to produce raffle ticket numbers (one per volunteer). Students record their number and come to the front of the room.
Remarks
- Thank you, volunteers! Let's figure out if any of you have the winning number for this instance of the problem. I'm going to ask you one by one to show your number and we will compare it with the winning number.
Teaching Tip
Before class, choose your own winning number (a number between 0-999), or alternatively use the Ticket Generator yourself!
Do This: Each volunteer reveals their number and compares it to the winning number.
Prompt 1: How many steps did it take to find out if anyone had the winning ticket? What is the greatest possible number of steps it could take for this instance?
Prompt 2: What if we had six volunteers? The whole class? The whole school? What is the pattern here?
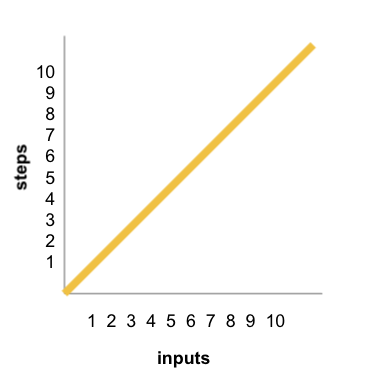
Display: Look at the chart as a class and examine the graph. The graph visualizes the pattern the class discussed.
| Inputs | Steps |
|---|---|
| 3 | 3 |
| 6 | 6 |
| 10 | 10 |
| 100 | 100 |
Remarks
- Now let's try a different way to search.
Group: Place students in groups of two.
Do This: With a partner, students use the Ticket Generator to create seven random numbers that are recorded, such as on sticky notes. Students organize the results in numerical order. Students choose one extra number as the "winning number" and write that number down on a separate sticky note.
Challenge: Students work with their partner to write an algorithm to search for their winning number. Make sure the rules are displayed.
- The search can start at any of the numbers.
- You can "jump" over numbers. In other words, you don't need to search the stickies in order.
- You can determine which numbers to search next based on the current number you are checking.
- The goal is to make the determination in the least steps possible, but don't forget your number could be anywhere in the list - what is the worst possible case? What is the greatest number of comparison steps it would take to find any number in your list using your current algorithm?
Discuss: Students share their algorithms with another group and determine which one runs faster, depending on the number of steps it takes to find a number in the list.
Teaching Tip
It's important for students to think about this problem as looking for the number in the worst possible situation. In other words, what is the least amount of steps it would take to definitively cross off every option?
Do This: Students return to their partner and now run this given algorithm, shown below, step by step. As they are doing this, they should think about whether or not this algorithm runs faster (has less steps) than their own algorithms.
- Find the middle number in the list. Compare that number to the given number. If the number is less than the given number, remove all of the cards to the right (including the middle number). If the number is more than the given number, remove all of the cards to the left (including the middle number).
- Find the middle number in this shorter list. Follow the instructions in Step #1 for comparing.
- Find the middle number in this new shorter list. Follow the instructions in Step #1 for comparing.
- This search algorithm is known as Binary Search. Let's see it in action.
Do This: As a class, find the number 705 in this list: 117, 232, 245, 410, 705, 716, 833. Follow the steps below, and discuss each step as it is happening.
- Find the number in the middle (410) and compare it with the given number (705). The given number is greater than the middle number, so remove the middle number and all to the left.
- Find the number in the middle of the numbers left (716), and compare it with the given number (705). The given number is less than the middle number, so remove the middle number and all to the right.
- Find the number in the middle of the numbers left (there is only one!), and compare it with the given number. The given number is equal to the middle number. We have found our number!
- Binary search only works with a sorted list of numbers. This allows us to remove options from the search after we've made a decision. In other words, if we know the number is greater than 410, we can remove all numbers less than or equal to 410 and we don't have to manually check those numbers one by one.
Do This: Display the table and graph below. Have students work out a few of the instances in the table to see how they arrive at the listed number of steps. Students copy the table and chart into their journals.
| Inputs | Steps |
|---|---|
| 1 | 1 |
| 3 | 2 |
| 5 | 3 |
| 7 | 3 |
| 9 | 4 |
| 15 | 4 |
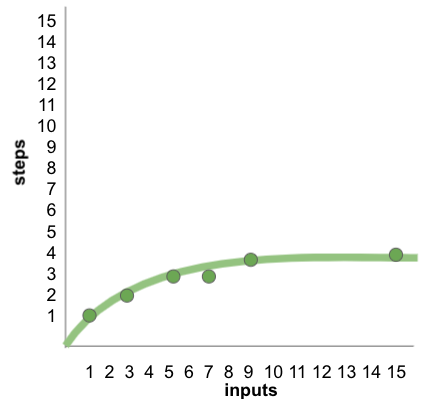
Question: Look at the table for Binary Search again. If we wanted to store the number of inputs in each row as a binary number, how many bits would each of the numbers need?
For Binary Search, for each instance the number of steps it takes to run is equal to the number of bits required to represent the input.
Teaching Tip
Binary Search with Even Numbers: What if there is no middle number while performing a step in Binary Search? Students can come up with a protocol for this like: if there is no middle number, compare the number on the right.
Hard Concepts: The relationship between binary numbers and binary search is a tricky concept! It's ok if students don't fully understand. What's most important is what is revealed next: Binary Search is more efficient than Linear Search.
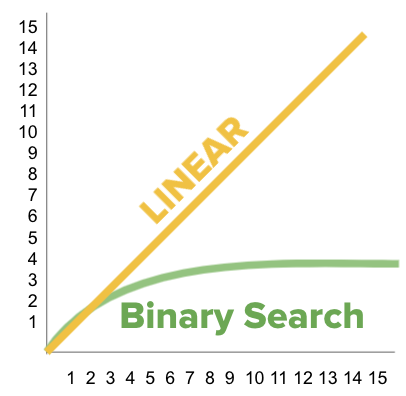
Display: Show students the graph below, which displays the two search algorithms we've explored.
The first is linear. As we add more inputs, the number of steps grows at the same rate.
The second represents what happens with Binary Search. It grows at a much slower rate! Binary Search is faster than Linear Search, BUT the data must be sorted.
Remarks
- Both Binary Search and Linear Search find the answer to our search problem. However, one option is much faster than the other: Binary Search, although it requires that the numbers are sorted first.
Wrap up (10 Minutes)
Prompt: If I had one input, which algorithm would I use to get my answer with the fewest amount of steps? What if I had five? What about one hundred?
Discuss: Have students think about their answers on their own, then share with a partner, and then finally discuss responses with the entire room.
Discussion Goal
- For one input, either Binary Search or Linear Search would be appropriate. Students may argue for Linear as it does not need to first be sorted.
- For five inputs, it's clear that Binary Search is fastest, although it only saves two steps over Linear Search. This is all the more true with one hundred inputs, which only takes seven steps (Binary number for 100 inputs: 1100100, 7 bits in total) compared to Linear Search's one hundred steps.
Remarks
- Computer scientists don't just think about "code", they think about problems and the algorithms that solve them. In this unit we're going to explore what makes two problems, or two algorithms, similar or different from one another, and the way computer scientists talk about them. Not only will you be a better programmer, but you'll get to work on some really interesting problems along the way.
Journal: Students add the following vocabulary words and definitions to their journals:
- Efficiency: a measure of how many steps are needed to complete an algorithm
- Linear Search: a search algorithm which checks each element of a list, in order, until the desired value is found or all elements in the list have been checked.
- Binary Search: a search algorithm that starts at the middle of a sorted set of numbers and removes half of the data; this process repeats until the desired value is found or all elements have been eliminated.
- Well done! It's clear that there are many algorithms we can use to search for an item in a list. Some are faster, or more efficient, than others. In the case of Binary Search, the larger the list we are searching through, the greater the efficiency in using this algorithm instead of Linear Search.
Assessment: Check for Understanding
For Students
Open a word doc or google doc and copy/paste the 2 following question.
Question 1
What is the third step using Binary Search to look for the number 32 in this list: 1, 2, 3, 4, 10, 11, 16, 25, 32, 33, 45, 47, 51, 69, 75 ?
- Compare the number 4 to the given number.
- Compare the number 25 to the given number.
- Compare the number 33 to the given number.
- Compare the number 47 to the given number.
Question 2
Which of the following is true of two algorithms designed to solve the same problem?
- If two algorithms solve the same problem they must have the same efficiency.
- If two algorithms solve the same problem they must have different efficiency.
- For any given problem there is a single algorithm that can solve it with a single efficiency.
- It is possible for two algorithms with different efficiencies to solve the same problem.
Standards Alignment
- CSTA K-12 Computer Science Standards (2017): 3B-AP-10, 3B-AP-11
- CSP2021: AAP-2.O.5
- CSP2021: AAP-2.P.1, AAP-2.P.2, AAP-2.P.3
- CSP2021: AAP-4.A.1, AAP-4.A.2, AAP-4.A.3, AAP-4.A.4, AAP-4.A.5, AAP-4.A.6
Next Tutorial
In the next tutorial, we will discuss Code.Org Unit 6 Lesson 3, which describes Learn why onLesson 4thm is more efficient than another.