Algorithms - Lesson 4: The Limits of Algorithms
Overview
Students explore the limits of what algorithms are able to compute. First they use a widget that exposes students to the Traveling Salesman Problem. After recognizing this problem can only be solved using an unreasonable time algorithm the develop their own good enough solutions that run more efficiently. Later in the lesson students watch a video about undecidable problems for which no algorithm can ever be developed to solve them.
Goals
Students will be able to:
- Determine if an algorithm runs in unreasonable time.
- Develop a heuristic to solve a problem.
- Distinguish between decision problems and optimization problems.
- Explain the existence of undecidable problems
Purpose
Prior to this lesson students have learned about the efficiencies of different algorithms and have considered the difference between reasonable and unreasonable algorithms. In this lesson they explore what happens when you reach that limit. In one instance the response is to accept good enough solutions that run more reasonably. In the other case the problem simply can't be solved at all.
Resources
Getting Started (5 minutes)
Prompt: What is the difference between a reasonable and unreasonable time algorithm?
Discuss: Have students think about their answers on their own, then share with a partner, and then finally discuss responses with the entire room.
Discussion Goal
Use this discussion to quickly review topics brought up in the previous lesson.
- Reasonable algorithms grow at a polynomial rate or slower. Unreasonable algorithms grow exponentially.
- The time to solve an unreasonable algorithm grows very quickly even for relatively small problem sizes.
Remarks
- This was a good reminder of what we learned last time. Unreasonable time algorithms just don't make sense to run. Today we're going to be thinking more about what happens when we reach the limits of algorithms, and how sometimes we can make compromises.
Activity (30 minutes)
Set Up: Each student needs to have their journal and a pen or pencil.
Activity: Today's activity introduces students to The Traveling Salesman Problem.
Discussion Goal
Running the Activity: This activity asks students to follow along as a core concept for programming is introduced. The model is typically that a term or concept is introduced and modeled and then afterwards students are encouraged to try it out on their own. Trying it out typically means they are writing information on a sticky note and sharing it with another group before discussing the results with the whole class.
To help you more easily prepare the activity and keep track of your instructions, detailed instructions have been included as speaker notes in the presentation. Here are some tips to help you throughout the presentation.
- There are opportunities throughout the presentation for students to actively engage. At these moments students should be making things with their manipulatives or using them to answer questions. Use these opportunities to check progress.
- The most important goal here is building a mental model. It is ok if students have some open questions that will get resolved over the subsequent algorithm lessons.
- Both you and students can use the "Key Takeaways" to check your understanding at the end.
Guided Activity
Slide: Traveling Salesman
Say: Today we are going to explore the Traveling Salesman Problem.
Slide: Presenting the problem
Prompt: How many different paths can you find to visit all of your friends' houses?

Do This: Students should sketch out different paths in their journals. Read through the rules together as a class.
Rules:
- You must start and end at your own house.
- You can only visit each house once.
Discuss: Students share their paths with a partner before discussing as a class.
Slide: Possible Paths
Say: Take a look at some of these paths on the screen. You may have similar ones in your journal.
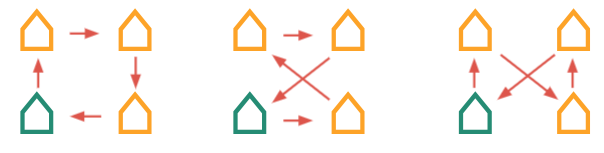
Prompt: What do you need to know to determine the best path?
Do This: Students should sketch out different paths in their journals. Read through the rules together as a class.
Slide: Same Possible Paths with Distances
Say: Distance! If we know the distance between each house, we can make a better decision about which path to take. In this example, the first option is shortest, so that's the path we would choose.
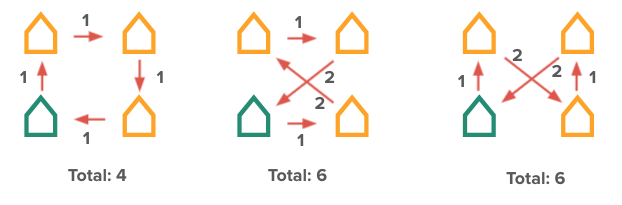
Slide: Many More Places to Visit
Prompt: What if we had a lot more places to visit? How would we determine the best path?

Discussion Goal: The goal here is for students to come to the realization that they would need to explore all possible paths in order to determine which one is the best.
Slide: The Traveling Salesperson Problem
Say: This is known as the Traveling Salesman Problem. For each new place to visit, the number of options for possible paths increases factorialy.
| Number of Houses to Visit | Number of Steps to Check for the "Best" Path |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5,040 |
| 8 | 40,320 |
| 9 | 362,880 |
| 10 | 3,628,800 |
Slide: Factorial Fun: n!
Say: A factorial function is written with the letter "n" followed by an explanation point. Here's how n! works: Multiply all whole numbers from the given number down to the number 1.
Note: Talk through the examples and the previous table. The goal here isn't for students to memorize the math, but to understand that with each new house added, the number of potential paths that have to be checked expands very quickly.
Here's how n! works:
Multiply all whole numbers from the given number down to the number 1.
For example:
Instance: 4 houses to visit.
4 times 3 times 2 times 1 = 24
Instance: 7 houses to visit.
7 times 6 times 5 times 4 times 3 times 2 times 1 = 5,040
For 10 houses you need to check 3,628,800 possible paths! That's a lot!
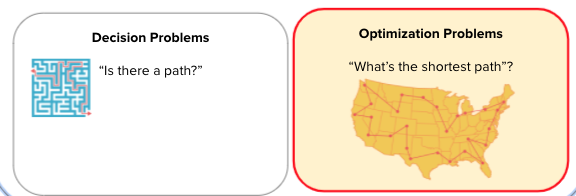
Slide: Problems
Say:The Traveling Salesman is an Optimization Problem. It's not a Decision Problem. We know there is a path. Now we must determine which is the shortest or most efficient path.
Problems:Any task that may (or may not) be solved with an algorithm. Sorting a list is a problem. Sorting the list (2, 3, 1, 7) is an instance of that problem.
Slide: Traveling Salesperson Solution
Say: The Traveling Salesman Problem can be solved with an algorithm, which checks each possible option.
BUT, it would take massive amounts of computing power to compare every single option, especially as the number of homes to visit (otherwise known as nodes) increases.
Therefore, it would take an unreasonable amount of time for the solution to be calculated for most instances of the problem.
Slide: Welcome to heuristics
Say: Welcome to heuristics! Heuristics provide a good enough solution to a problem when an actual solution is impractical or impossible.
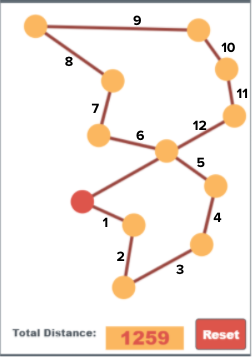
Open a Project: Students now open the Lesson4_TravelingSalespersonWidget project in the Unit 6 folder of the CSP-Widgets repository. They will use the Traveling Salesman Widget to find the "best" path to visit all nodes.
In their journal, students should write down a plan or heuristic for choosing a good path.
Discuss: In pairs, students should share their heuristics and make adjustments to their own as needed.
Open a Project: Now students navigate to Level 3 and use the Lesson4_TravelingSalespersonWidget project in the Unit 6 folder of the CSP-Widgets repository. Students test their heuristic on this widget, keeping a log in their journal of the distance for the path their heuristic finds and the best distance the student finds not using the stated heuristic (i.e. clicking around, or "brute force").
Note: Click reset to try different paths on the same level. Click "New Level" to generate at new random assortment of nodes.
Prompt: How did you create your heuristic? Did you change your heuristic after testing it out?
Discussion Goal
Tease out what factors students used to create their heuristics.
Discuss: Call on several students to share their heuristics. As a class, discuss which heuristic we think is best, and will give us a "good enough" result for most cases.
Discuss: Discuss whether or not this heuristic is "good enough".
Discussion Goal
There are times when the Next-Closest heuristic will not provide the best option, but on average it's a good option.
- Students can reflect back on the paper route problem from earlier in the class. This may have been the option they first suggested.
Discuss: Call on several students to share their heuristics. As a class, discuss which heuristic we think is best, and will give us a "good enough" result for most cases.
Remarks: The Traveling Salesman Problem is an optimization problem. We are attempting to find the best path.
It's also unreasonable because there is not an algorithm that can solve the problem in a reasonable amount of time.
We need to use a heuristic to come up wtih a solution that is "good enough" for most instances of the problem.
Undecidable Problems
Remarks: We've learned how we address unreasonable problems. Before we finish our study of problems let's learn about one more type, problems that no algorithm will ever be able to solve. This video is a little tricky, but it gives you a good sense for the way this problem shows up.
Teaching Tip
Do I Need to Understand the Halting Problem: Students don't actually need to understand the Halting Problem or the proof in this video. The main ideas are covered in the takeaways and are fairly simple. There are a few problems, most notably "will this code run?" that we've proven there is no algorithm that will ever be able to determine the correct answer in every case. The proof is interesting but if you are short on time you may opt to skip the video.
Do I Need to Understand the Halting Problem: Students don't actually need to understand the Halting Problem or the proof in this video. The main ideas are covered in the takeaways and are fairly simple. There are a few problems, most notably "will this code run?" that we've proven there is no algorithm that will ever be able to determine the correct answer in every case. The proof is interesting but if you are short on time you may opt to skip the video.
Click on the following link to learn about the Halting Problem (Supplemental)
Takeaways
There are some problems we’ve proven that no computer will ever be able to solve. The Halting Problem is a very famous example and in general we call these problems undecidable.
Wrap up (10 Minutes)
Prompt: Why is a heuristic acceptable when it doesn't always produce the "best" result?
Discuss: Have students think about their answers on their own, then share with a partner, and then finally discuss responses with the entire room.
Discussion Goal
Answer: A heuristic is used when it's impossible or impractical to use an algorithm to solve a problem. Therefore, we need something that is good enough on average for most instances. This is where a heuristic shines.
Remarks
Great! Heuristics are handy in every day life. Think about using mapping software to find the best route to a destination!
Assessment: Check for Understanding
For Students
Open a word doc or google doc and copy/paste the 2 following questions.
Question 1
In which of the following situations is it most appropriate to use a heuristic solution?
- a. The only algorithms that provide exact solutions run in linear time.
- b. The problem has been identified as undecidable.
- c. The only algorithms that provide exact solutions run in unreasonable time but exact solutions are not necesssary.
- d. Two diffferent algorithms have been identified that solve the problem in reasonable time.
Question 2
Problems that are undecidable and algorithms that are unreasonable both touch on the limits of the kinds of computing that a computer can accomplish. In your own words, explain the difference between undecidable problems and unreasonable time algorithms.
Standards Alignment
- CSTA K-12 Computer Science Standards (2017): 3B-AP-11
- CSP2021: AAP-4.A.2, AAP-4.A.8, AAP-4.A.9
- CSP2021: AAP-4.B.1, AAP-4.B.2, AAP-4.B.3
Next Tutorial
In the next tutorial, we will discuss Code.Org Unit 6 Lesson 5, which describes Explore the benefits and limitations of parallel and distributed computing.