Algorithms - Lesson 3: Unreasonable Time
Overview
Students investigate two different types of raffles that highlight the way seemingly small problems can quickly grow large. The first raffle asks students to hunt for pairs of tickets that add to a target value. The second raffle asks students to hunt for any group of tickets that adds to a target value. After trying out each raffle live students will try to figure out the patterns for how many total combinations need to be checked in each. At the end they discuss the difference between reasonable and unreasonable algorithms based on their experiences.
Goals
Students will be able to:
- Explain the difference between problems that run in a reasonable time and those that do not
- Explain how both formal mathematical reasoning and informal measurement can be used to determine an algorithm's efficiency
Purpose
This lesson explores some tricky mathematical concepts in a hands on and interactive way. Building off the raffle analogy used in the previous lesson, it gives students an experience with two types of problems that grow quickly in size, though as they'll see one grows much faster than the other. This lesson should give students a sense of how computer scientists use mathematics to think about problems without relying too heavily on mathematical background that not all students may have.
Resources
Getting Started (5 minutes)
Prompt: What does it mean to say one algorithm is "more efficient" than another?
Discuss: Have students think about their answers on their own, then share with a partner, and then finally discuss responses with the entire room.
Discussion Goal
This prompt is a review from the previous lesson. Students should be free to refer to notes or their journals. You might hear the following points.
- One algorithm requires fewer steps to complete than another
- "The line for one algorithm curves below the other"
- More efficient algorithms are much more helpful as input size grows. The amount of work grows more slowly.
Remarks
- Yesterday we started looking at how computer scientists might compare two algorithms that solve the same problem. Today we're going to look at two different problems. They may seem similar but as we'll see they actually are much harder to solve than either of the two we saw yesterday. The question will be "how much harder"? Let's get to it!
Activity (30 minutes)
Open a Project: Have students re-open the Lesson2_TicketGenerator project in the Unit 6 folder of the CSP-Widgets repository. Students will use this to randomly generate ticket numbers for today's activity.
Problem #1 - The Pair Raffle: Every student will generate a ticket. Any pair of students win the raffle if their two tickets add to the winning number. The winning number is 1000.
Do This:
- Generate a ticket
- Silently move around the room
- See if you're part of a winning pair!
Circulate: Give students a couple of minutes to walk around the room seeing if they can find a partner with which they can win the raffle. After a couple of minutes have them return to their desks. If there are any winners feel free to celebrate.
Teaching Tip
Both because it helps give students a sense of the problem space and because it's fun to run a raffle, you should run both the pair raffle and the group raffle in your classroom. Here's some helpful tips.
- Insist that students check for the pair raffle silently. For this one it's very easy to just yell out what number you would pair with and lose the opporuntity to see how many total checks are necessary if they can just all yell from their seats.
- The group raffle doesn't necessarily need to be silent. As students will see, it's an incredibly difficult problem and they're going to need to do a lot of checking even if they're able to talk out loud.
- Think ahead about whether you actually want to award winners of the raffles. It's pretty unlikely that there will be a winner.
- There's a pretty good chance that no one will win either raffle.
- As computer scientists we're getting better at thinking about problems and algorithms. We also saw last time that we can use a little mathematical reasoning to decide if one algorithm is more efficient than the other. Let's do a little work on these two raffles to see if our intuitions are correct.
- Alright, that was interesting. Let's try out a different version of the raffle. Last time I made you work silently so that we got a better sense of how many checks needed to happen. This time we're going to run a group raffle, but I'll let you talk out loud if you want.
Problem #2 - The Group Raffle: Each student generates a new ticket. The winners are any group of students (from one ticket up to all of them) that adds up to the winning number. The winning number is 2500.
Do This:
- Generate a ticket
- Move around the room (you can talk this time)
- See if you're part of a winning group!
Circulate: Give students a couple of minutes to walk around the room seeing if they can find a group with which they can win the raffle. After a couple of minutes have them return to their desks. If there are any winners feel free to celebrate.
Prompt: Which raffle felt like it was more difficult to check? Why?
Discuss: Have students discuss this prompt with a neighbor. Then have a few students share out their reflections.
Discussion Goal
This discussion is primarily designed to get quick reactions from students to motivate the second big activity in this lesson. Students will likely note that the group raffle felt a lot harder to check, even with the ability to talk. That said, there's no wrong answers at this point. You're about to check their intutions mathematically.
Remarks
Distribute: Distribute copies of Unreasonable Time - Activity Guide
Problem #1 - The Pair Raffle: Ask students to fill out the first page where they must figure out the total number of pairs for different sized "pair raffles". This may take several minutes and require students to draw pictures.
Problem #2 - The Group Raffle: Ask students to fill out the second page where they must figure out the total number of groups for different sized "group raffles". This may take several minutes and require students to draw pictures.
Share Responses: Ask students to share their responses with another group.
Display: Look at the chart as a class and examine the graph. The graph visualizes the pattern the class discussed.
| Tickets | Checks |
|---|---|
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
| 8 | 28 |
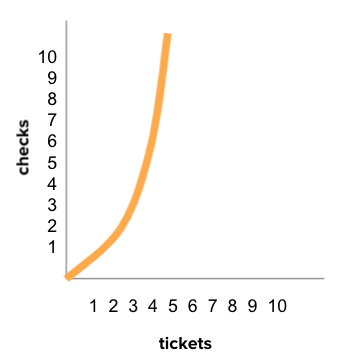
The exact formula for this relationship is (n^2 - n)/2 You don’t need to know that formula, but you should know that because of the "n-squared" term the graph curves up. Any algorithm whose efficiency includes an n2, n3, n4 … is called polynomial.
| Tickets | Checks |
|---|---|
| 2 | 3 |
| 3 | 7 |
| 4 | 15 |
| 5 | 31 |
| 8 | 255 |
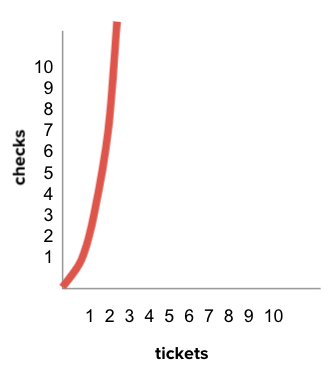
The exact formula for this relationship is (2^n) - 1 You don’t need to know that formula, but you should know that because of the "2 to the n" term the graph curves up very quickly. Any algorithm whose efficiency includes an 2n, 3n, 4n … is called exponential.
Prompt: Polynomial and exponential both curve up. Why do you think only exponential is considered "unreasonable"?
Discuss: Briefly ask students for their ideas why before showing them the following slides. Exponential curves grow extremely quickly. You simply can't build a computer fast enough even for relatively small raffle sizes.
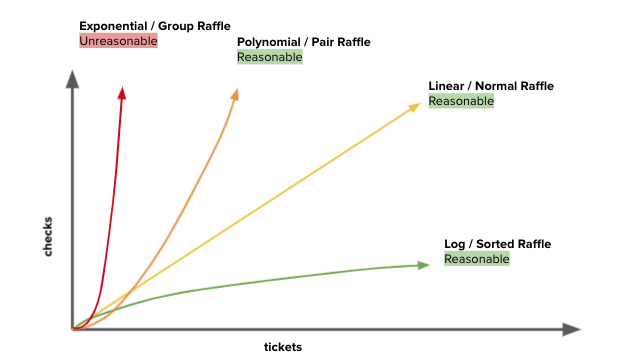
| Tickets | Sorted Raffle (log) | Normal Raffle (linear) | Pair Raffle (polynomial) | Group Raffle (exponential) |
|---|---|---|---|---|
| 10 | 4 Checks | 10 Checks | 100 Checks | 1,024 Checks |
| 20 | 5 Checks | 20 Checks | 400 Checks | 1,048,576 Checks |
| 100 | 7 Checks | 100 Checks | 10,000 Checks | 1.26*10^30 Checks |
| 1000 | 10 Checks | 1000 Checks | 1,000,000 Checks | 1.07*10^301 Checks |
| 10,000 | 14 Checks | 10,000 Checks | 100,000,000 Checks | 2.00*10^3010 Checks |
| 100,000 | 17 Checks | 100,000 Checks | 1.00*10^10 Checks | 9.99*10^30102 Checks |
Polynomial is bad but exponential gets unreasonably large extremely quickly.
Note that 1.07*10^301 Checks (1000 tickets in a group raffle) is more checks than atoms in the entire universe!
Wrap up (10 Minutes)
Prompt: Your school is considering running the group raffle at an upcoming assembly to give away a prize. Write a brief explanation of what advice you would give them.
Discuss: Have students think about their answers on their own, then share with a partner, and then finally discuss responses with the entire room.
Discussion Goal
Use this discussion to reinforce vocabulary introduced in the slides and make sure they have understood the main concepts of the day. Students should be able to explain with the term reasonable, unreasonable, and exponential, why running a group raffle in a school of most sizes is impossible.
Remarks
- The group raffle is just one example of an algorithm that is "unreasonable". It grows exponentially and so we'd never want to run it at our school. Next time we'll talk more about what to do when we encounter unreasonable problems.
Journal: Students add the following vocabulary words and definitions to their journals:
- Unreasonable time: Algorithms with exponential or factorial efficiencies are examples of algorithms that run in an unreasonable amount of time.
- Reasonable time: Algorithms with a polynomial efficiency or lower (constant, linear, square, cube, etc.) are said to run in a reasonable amount of time.
Assessment: Check for Understanding
For Students
Open a word doc or google doc and copy/paste the 2 following questions.
Question 1
Which of the follow efficiencies would be considered unreasonable?
- a. 2^n
- b. 2n
- c. n^2
- d. n^20
Question 2
A team of programmers is trying to determine the efficiency of a piece of code. They run the code with inputs of different sizes and also record the number of iterations through the core block of code. The data is recorded in the table below.
| Input Size (Tickets) | Iterations (Checks) |
|---|---|
| 10 | 200 |
| 20 | 400 |
| 30 | 600 |
| 40 | 800 |
| 50 | 1000 |
| 100 | 2000 |
Based on the data provided, does this algorithm run in a reasonable or unreasonable time? Explain your answer
Standards Alignment
- CSTA K-12 Computer Science Standards (2017): 3B-AP-11
- CSP2021: AAP-4.A.4, AAP-4.A.7
Next Tutorial
In the next tutorial, we will discuss Code.Org Unit 6 Lesson 4, which describes Learn why one algorithm is more efficient than another.